Hi,
Sobat ISOMATH!
Jika
di SMP kita sudah mengenal Persamaan Linear Satu Variabel, maka di SMA kita
juga diajarkan dengan hal yang serupa. Namun, lebih kompleks dibanding
sebelumnya. Persamaan Linear Satu Variabel atau sering dikenal dengan PLSV yang
akan di pelajari kali ini adalah PLSV yang memuat Nilai Mutlak. Apa itu nilai mutlak? Yuk, kita pelajari bersama!
Nilai mutlak
disebut juga nilai absolut atau modulus.
Untuk
mempermudah kita belajar nilai mutlak, coba perhatikan garis bilangan berikut!
Dari ilustrasi pada gambar 1, kita bisa lihat
bahwa jarak dari bilangan nol ke bilangan 4 adalah 4 satuan. Sedangkan, jarak
dari bilangan nol ke bilangan -4 juga 4
satuan. Jarak inilah yang disebut nilai
mutlak.
Sehingga
secara geometris, nilai mutlak (nilai absolute) merupakan suatu jarak
antara bilangan tertentu dengan nol pada garis bilangan real. Karena jarak,
maka nilainya selalu positif (tidak ada yang negatif).
Berikut
ini definisi dari Nilai Mutlak.
Berdasarkan
definisi di atas, nilai mutlak bilangan positif atau nol adalah bilangan itu
sendiri dan nilai mutlak bilangan negatif adalah lawan dari bilangan tersebut.
Contoh Soal
1. |3|=
...
Penyelesaian:
karena 3 > 0 maka
hasilnya bilangan yang ada di dalam nilai mutlak itu sendiri
Jadi |3|= 3
2. |-5|=
...
Penyelesaian:
karena -5 < 0 maka
hasilnya kebalikan dari bilangan yang
ada di dalam nilai mutlak
Jadi |-5|= -(-5)= 5
3. |0|=
...
Penyelesaian:
karena 0 = 0 maka |0|= 0
Jadi,
jelas nilai mutlak setiap bilangan real selalu bernilai positif atau nol.
Bagaimana
sudah sedikit paham tentang nilai mutlak?
Sekarang,
bagaimana jika bilangan yang ada di dalam nilai mutlak berbetuk aljabar?
Tenang
sobat. Jangan panik dulu! Yuk, kita sama-sama fokuskan diri untuk mulai
memperhatikan penjelasan berikut ini.
Dalam menyelesaikan PSLV yang melibatkan nilai mutlak dengan menggunakan definisi, akan sangat membantu jika bentuk |ax + b| kita jabarkan menjadi seperti berikut
Contoh Soal Persamaan Linear Satu
Variabel yang Melibatkan Nilai Mutlak
Tentukan
himpunan penyelesaian dari persamaan nilai mutlak berikut ini!
1. |2x-1|= 7
Penyelesaian:
2.
|3x-6|= 0
Penyelesaian:
Perlu kalian ingat, jika hasilnya = 0 maka hanya punya satu penyelesaian. Untuk membuktikannya, yuk simak berikut ini!
3.
|x+5|= -6
Penyelesaian:
Perlu kalian ingat, jika hasilnya
= bilangan negatif maka tidak punya penyelesaian. Untuk membuktikannya, yuk
simak berikut ini!
4.
-5|x-7|+2= -13
Penyelesaian:
Supaya lebih mudah, sederhanakan terlebih dahulu persamaan nomor 4. (Apabila tidak disederhanakan juga tidak masalah)
Perhatikan persamaan |x-7|= 3.
Jadi, HP={4,10}
Selengkapnya
bisa ditonton di youtube channel isoMATH
Supaya
kita terlatih dalam mengerjakan soal yang berkaitan dengan PLSV melibatkan
nilai mutlak, coba deh latihan soal berikut ini!
Siapkan
alat tulis kalian dan kerjakan!
Latihan Soal
Tentukan
himpunan penyelesaian dari persamaan nilai mutlak berikut ini!
Pengen
tahu pembahasan latihan soal di atas?
Sobat
bisa mengetahui pembahasannya hanya di youtube channel isoMATH
Terima kasih sudah berkunjung di blok ini. Semoga konten ini dapat bermanfaat bagi sobat semua.
Semangat belajar !!! J








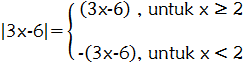







Comments
Post a Comment